Skip to content

Bit Manipulation

In this section, we will try to understand the following:

  • base, conversion between bases
  • representing integers (optional)
  • bit operators

这一章结束之后，你可以回答,

  • how to convert between base 10 to base Y (Y can be 2, 8, 16 etc)?

1. Base

Base也就是我们熟悉的2进制，8进制，16进制等等。这些都是base。是一种表达数字的方式方法，我们人类最熟悉的是十进制,

先来看两个例子123.45 in base 10,

\[ 123.45 = 1*10^2 + 2*10^1 + 3*10^0 + 4*10^{-1} + 5*10^{-2} \]

再来看base-8转换到base 10，

\[ 720.5_{\left(8\right)} = 7*8^2 + 2*8^1 + 0*8^0 + 5*8^{-1} = 464.625_{\left(10\right)} \]

看完这两个例子后，我们来对应weight在base中的意义，123.45的weights为

  • 小数点后有两位, \(10^{-1}\) and \(10^{-2}\).
  • 小数点前有三位, \(10^0\), \(10^1\), and \(10^2\).

由这些weights就能组成数字.

1.1 Conversion Between Bases

人类十进制，计算机二进制，八进制(octal)，十六进制(hexadecimal)。这些都是常用的base. 比如十进制转化到二进制, 50 in base-10 to base-2,

50 / 2 = 25; 50 % 2 = 0
25 / 2 = 12; 25 % 2 = 1
12 / 2 = 6; 12 % 2 = 0
6 / 2 = 3; 6 % 2 = 0
3 / 2 = 1; 3 % 2 = 1
1 / 2 = 0; 1 % 2 = 1

然后traverse the remainders from bottom to top, we get \(50_{(10)} = 110010_{(2)}\). 对于小数，我们可以用类似的方法，不过是乘以2. 比如0.6875 to base-2,

0.6875 × 2 = 1.375 with integer 1
0.375 × 2 = 0.75 with integer 0
0.75 × 2 = 1.5 with integer 1
0.5 × 2 = 1 with integer 1

Traverse the integer part from top to bottom, we get \(0.6875_{(10)} = 0.1011_{(2)}\).

Warning

A finite fraction in one base may become infinite in another case. 比如1/3 in base-10 is 0.3333...，但是在base-3中是0.1.

2 Representing Integers

计算机用binary, 每一个digit(位)，用计算机术语叫做bit, can only be 0 or 1. 也就是说，m digits的二进制，能表示的数字是\(2^m\) in base-10. 或者说, \(2^m\)表示的是可能性.

Tip

对于可能性的理解，你可以想象成你抛硬币，硬币正反两面对应0和1. 你抛m次硬币，你有\(2^m\)种可能性. 同理for m digits in a row like _,_,_...,_,_, you have \(2^m\) possibilities.

bit单位太小了，所以有了1 byte = 8 bits. bytes能表达的,

  • 1-byte number, i.e. 8 bits with \(2^8\) possibilities, 0 to 255.
  • 2-byte number, i.e. 16 bits with \(2^{16}\) possibilities, 0 to 65535.
  • 4-byte number, i.e. 32 bits with \(2^{32}\) possibilities, 0 to 4294967295.
  • 8-byte number, i.e. 64 bits with \(2^{64}\) possibilities, 0 to 18446744073709551615.

3. Signed and Unsigned Integers

我们之前的讨论，包括了正整数和小数，但没讨论过负数。计算机需要表达正数和负数，因此有一个概念叫sign bit, 假设我们有一个1 byte, 如下图所示

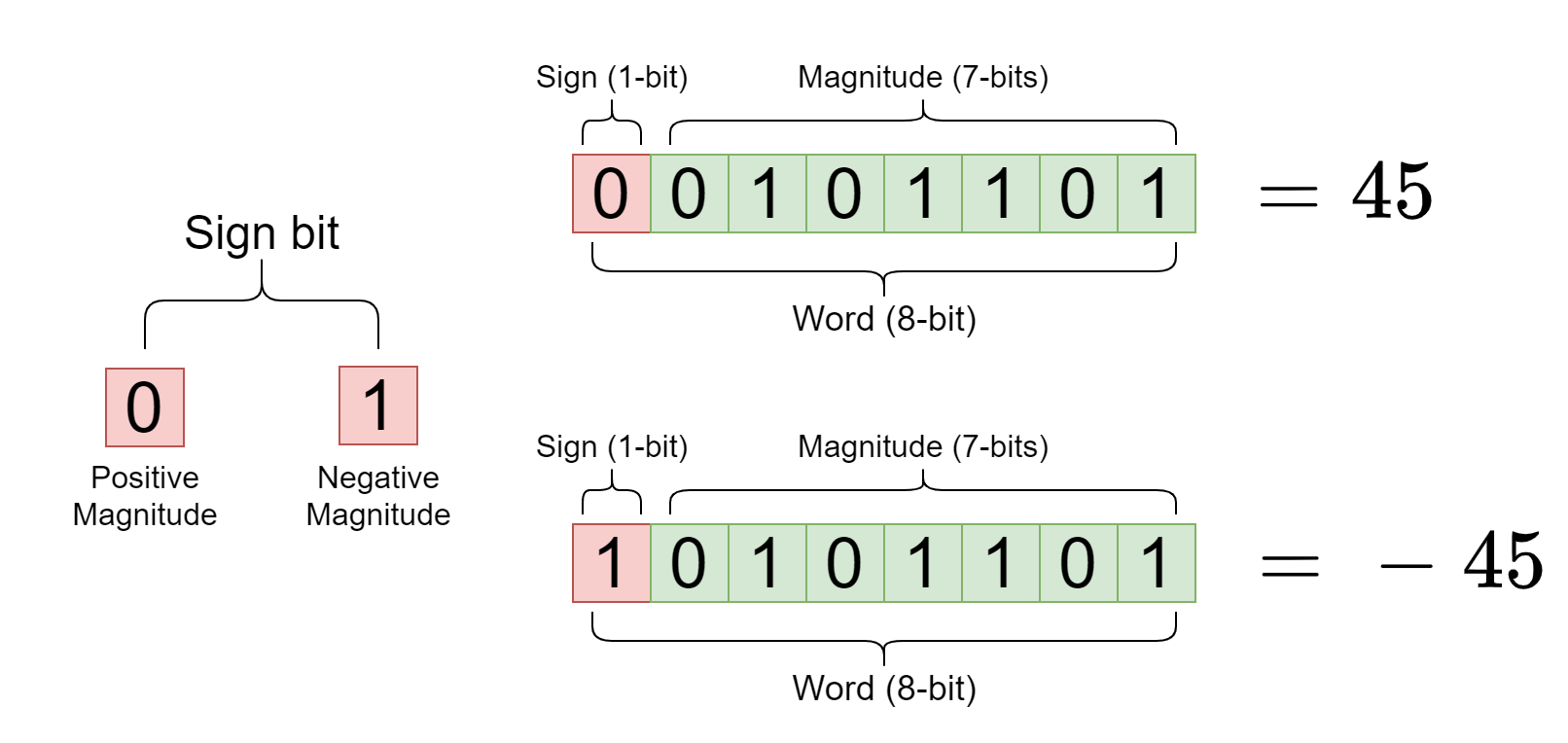
其中1 byte中的第一位是sign bit, 0表示正数，1表示负数。剩下的7位是magnitude bits, 用来表示数字的大小。也就是说，同样的一个数据类型，根据定义不同，能表示的数字范围也不同。比如,

  • 1 byte signed integer. 因为\(2^7\) = 128 for magnitude bits, 然后sign bit表达0或者1， 所以推理出-128 to 127
  • 1 byte unsigned integer. \(2^8\) = 256, 所以0 to 255.

由以上，我们可以总结出,

  • n bits signed integer, \(-2^{n-1}\) to \(2^{n-1}-1\). For unsigned integer, 0 to \(2^n-1\).

3. The Original Code, Inverse Code and Complement Code

3.1 Machine Number and Truth Value

先得知道俩概念， machine number and truth value.

  • machine number: The binary representation of a number in a computer is called its machine number. It's a signed number.
  • truth value: 用来区分和纯2进制的区别。

比如，the truth value of 00000010 is +2 and truth value of 10000010 is -2. 但real value of 10000010 is 130.

3.2 Original Code

The original code is the sign bit of the machine number plus the absolute value of the truth value of the machine number.

The original code for +10 is 00001010 and for -10 is 10001010.

3.3 Inverse Code

The inverse code 是derived from original code. 定义为:

  • 对于非负数, inverse code is the same as the original code.
  • 对于负数, inverse code flip every bit of the original code except the sign bit. flip的定义为0变成1, 1变成0.
- original code inverse code
+10 00001010 00001010
-10 10001010 11110101

3.4 Complement Code

The complement code 是derived from the inverse code. 定义为:

  • 对于非负数, complement code is the same as the inverse code.
  • 对于负数, complement code is the inverse code plus \(1_{\left(2\right)}\).
- original code inverse code complement code
+10 00001010 00001010 00001010
-10 10001010 11110101 11110110

3.5 有啥用?

主要是为了方便人脑计算.

4 Bit Operations

一共有6种bit operations, AND, OR, XOR, negation, left shift and right shift 如下表

Operation Symbol Description
AND & 两个bit都是1，结果是1
OR \(\mid\) 两个bit有一个是1，结果是1
XOR ^ 两个bit不一样，结果是1
NOT ~ flip bit
Left Shift << 左移
Right Shift >> 右移

4.1 AND, OR, XOR and Negation

The symbol for AND is &. 两个bit都是1，结果是1.

The symbol for OR is \(\mid\). 两个bit只要有一个是1，结果是1.

The symbol for XOR is ^ (python) but in math \(\oplus\). 两个bit不一样，结果是1, 比如

  • 0 \(\oplus\) 0 = 0
  • 0 \(\oplus\) 1 = 1
  • 1 \(\oplus\) 0 = 1
  • 1 \(\oplus\) 1 = 0

其实也可以用来表达venn's diagram. 代表着symmetric set difference, 也就是说，两个集合的差集，不包括交集. 比如\(A \oplus B = (A-B) \cup (B-A)\). 其实也就是exclusive or了.

The symbol for NOT is ~. flip bit.

  • ~0 = 1
  • ~1 = 0

Tip

For Negation, 你先求出原数的complement code, 然后加1.比如你有一个数，-1， 你先求1 in binary 0001, 然后flip bit, 1110, 然后加1, 1111. 或者用我们之前学的, 先学original code of -1, 10000001, 然后inverse code, 01111110, 然后complement code, 01111111.

你可以做点简单的exercise来理解这些操作.

4.2 Left and Right Shift

flowchart TD
shift[Shift Operation] 
dir[direction]
sign[whether it is signed or unsigned]
shift --> dir & sign

dir --> |left| left["left <<"]
dir --> |right| right["right >>"]

sign --> |signed| signed["logical shift"]
sign --> |unsigned| unsigned["arithmetic shift"]

For left shift <<, all binary bits are shifted to the left by a certain number of positions. The high bits are discarded and the low bits are filled with 0.

For right shift >>, all binary bits are shifted to the right by a certain number of positions. The low bits are discarded and,

  • for arithmetic shift, the high bits are filled with the highest bit, 最左边的bit, 也就是sign bit. 就是保留符号的shift.
  • for logical shift, the high bits are filled with 0. 也就是不保留符号的shift.

Warning

对于正整数，logical shift和arithmetic shift是一样的。但是对于负数，logical shift和arithmetic shift是不一样的。

-50 in binary is 11001110. 

flowchart TD
a[-50]
b[11110011]
c[00110011]

a -->|arithmetic right shift by 2 bits| b
a -->|logical right shift by 2 bits| c

b --> d[-13]
c --> e[51]

4.3 shift operation与乘除法的关系

这也是为什么我们要学这玩意.

4.3.1 left shift and multiplication

left shift << 对应着multiplication. 比如shift 29 by 2 bits is 116, which is same as 29 * 4. 实际上很好理解，因为we discard high bits and fill low bits with 0, 也就是说我们代表的可能性整体增加了\(2^2\). 29 in binary is 11101, shift之后是1110100, which is 116. 我们解刨一下29 = 11101, 代入weights,

\[ 29_{(10)} = 2^4 + 2^3 + 2^0 = 11101_{(2)} \]

We shift it to the left by 2,

\[ \begin{align} 1110100_{(2)} &= 2^6 + 2^5 + 2^2 \\ &= 2^2 (2^4 + 2^3 + 2^0) \\ &= 4 \times 29_{(10)} \\ \end{align} \]

这是以2为multiplier的情况，如果是以其他数为multiplier，可以用\(\sum 2^n\)的线性组合表示, 比如你想要一个数 a x 6, (a << 2) + (a << 1). 也就是\(2^2 + 2^1 = 6\)

Warning

但是要注意，如果乘法结果超过了数据类型能表示的范围，就会overflow. 比如32位的int, 2^31-1 = 2147483647, 2^31 = 2147483648, 超过了int能表示的范围.

4.3.2 right shift and division

arithmetic right shift >> 对应着division. 50经过2位arithmetic right shift, 得到12， 也就是\(\frac{50}{2^2}\), 这个只对正整数hold.

4.4 Properties of Bit Operations

Assuming signed integers,

- formulation description example
idempotent law \(a \& a = a, a \mid a = a\) 我operate我自己，还是我自己. -
commutative law \(a \& b = b \& a\), \(a \mid b = b \mid a\), \(a \oplus b = b \oplus a\) 交换律 -
associative law \((a \& b) \& c = a \& (b \& c)\), \((a \mid b) \mid c = a \mid (b \mid c)\), \((a \oplus b) \oplus c = a \oplus (b \oplus c)\) 结合律 -
distributive law \(a \& (b \mid c) = (a \& b) \mid (a \& c)\), \(a \mid (b \& c) = (a \mid b) \& (a \mid c)\),\(a \oplus (b \& c) = (a \oplus b) \& (a \oplus c)\), 分配律 -
De Morgan's law \(\sim (a \& b) = \sim a \mid \sim b\), \(\sim (a \mid b) = \sim a \& \sim b\) 德摩根定律 -

上述这些法则之外，加减乘除法也有对应的法则，比如

  • AND Operation:
    • \(a \& 0 = 0\),
    • \(a \& (-1) = a\),
    • \(a \& (\sim a) = 0\)
  • OR Operation:
    • \(a \mid 0 = a\),
    • \(a \mid (\sim a) = -1\)
  • XOR Operation:
    • \(a \oplus 0 = a\),
    • \(a \oplus a = 0\)
  • Negation Operation (flipping bits):
    • \(\sim 0 = -1\),
    • \(\sim (-1) = 0\)
  • Other Properties:
    • \(a \& (a-1)\) is to change the last 1 in the binary representation of a to 0.
    • \(a \& (-a)\) is to keep only the last 1 of the binary representation of a, and set the remaining 1s to 0.

这些properties对于理解bit manipulation和做bit的题目很有用.