Problem
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:
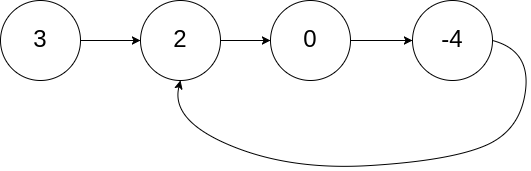
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Intuition
Recall the floyd's hare and turtle for cycle detection as illustrated in the figure below. If we label the length, we have the following
| symbol | description |
|---|---|
| \(L\) | length of the cycle |
| \(x\) | the distance from the head to the start of the cycle |
| \(y\) | the distance from the start of the cycle to the position they met |

If the hare is moving at a speed two-times faster than the hare, they will meet with each other at an arbitrary location inside the cycle. Now two things happen:
- bugs bunny starts to nap
- a dragon appears and starts to move at the same speed as the turtle from the head

Then the dragon and the hare will meet up at the start of the cycle. But how? Please see the proof section.

Math proof
Let's assume $$ \begin{align} d_{1} = x + y + n_1\times L \ d_{2} = x + y + n_2\times L \end{align} $$ where \(d_{1}\) and \(d_{2}\) are the distance covered by the turtle and the hare, respectively, and \(n_1\) and \(n_2\) are the distance number of cycles taken by the turtle and hare, respectively.
Since we know that the speed of hare is two times faster than the turtle and they start their racing at the head simultaneously. Then the distance traveled by the hare will be exactly two-times the distance traveled by the turtle, which means
$$
\begin{align}
2d_1 = d_2
\end{align}
$$
Then we substitute equations 1 and 2 into 2, $$ \begin{align} 2d_1 &= d_2 \ 2x + 2y + 2n_1L &= x + y + n_2L \ x + y + (2n_1 - n_2)L &= 0 \ x &= (n_2 - 2n_1)L - y \geq 0 \end{align} $$ where \(n_2,n_1 \in Z\)
From equations 7, we know \(L>y\) and \(x>0\), then we have
$$ k = n_2 - 2n_1 \geq 1 $$ where k is 大于等于1的正整数.
Let's do some trick with the equation 7 $$ \begin{align} x &= kL - y \ x &= \left(k-1\right)L + \left(L - y\right) \ \end{align} $$ where \(k-1\geq0\)
As we know, \(x\) is defined as the distance from the head to the start of the cycle. If dragon and turtle moving at the same speed, this means that the dragon will
- dragon travels \(x = \left(k-1\right)L + \left(L - y\right)\) to get to the start of the linked list
Let's look at the turtle, if we generalize when the turtle will travel from A (turtle met bug bunnys) to B (the start of the cycle), then $$ s_{turtle} = NL + (L-y) $$ where \(N\geq0\) and \(N\in Z\)
You realize that distance traveled by turtle \(s_{turtle}\) and dragon \(x\) is the same.Then dragon and the turtle will meet at the start of the cycle.

Solution
Optimal
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = head
fast = head
while fast and fast.next:
slow, fast = slow.next, fast.next.next
if slow == fast:
curr = head
while curr != slow:
curr, slow = curr.next, slow.next
return curr
# no cycle at all
return None
Brute force
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
hashset = set()
curr = head
while curr:
if curr not in hashset:
hashset.add(curr)
else:
return curr
curr = curr.next
return None