Problem
Given the root of a binary tree, return all root-to-leaf paths in any order.
A leaf is a node with no children.
Example 1:
1
/ \
2 3
\
5
Output: ["1->2->5" ,"1->3"]
Algorithm
The solution makes use of a stack data structure to traverse the binary tree in a depth-first manner. It maintains a stack of tuples, where each tuple contains a node and the path to that node from the root.
It then iteratively pops a tuple from the stack, checks if the node is a leaf node, and if so, appends the path to the list of paths. If the node is not a leaf node, it pushes its left and right children onto the stack with their respective paths.
The function returns the list of paths once the stack is empty.
# DFS # stack of tuples
Time complexity: O(n), each node visits exactly once
Space complexity: O(n)
性能优化
题目中将
if node.left:
# use str().join(iterable)
stack.append((node.left, '->'.join([path, str(node.left.val)])))
if node.left:
# use +
stack.append((node.left, path + '->' + str(node.left.val)))
The reason is that in python, it uses
- stack memory: to manage function calls
- heap memory: to store objects (garbage collector goes here)
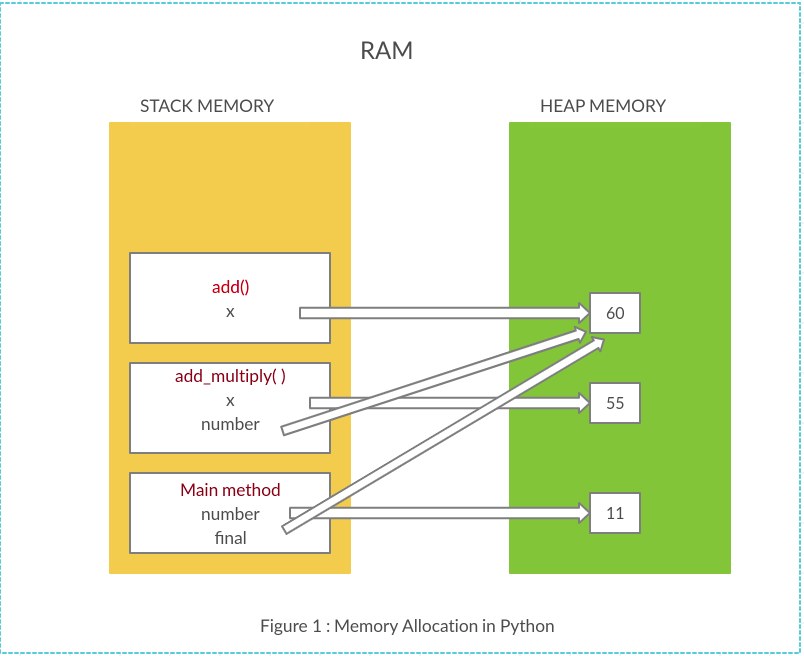
Since str() in Python is designed to be immutable, therefore if we use path + "->" + str(node.left.val), we create intermediate string variables, which will be stored in the heap.
As for the reason why the str() has been designed as immutable, there are two folds:
- In multi thread process, two thread may access the same string variables and do modification on it. If it's mutable, the state of string thread A accessing might not be the same as what thread B has seen.
- Also, it simplifies the implementation of certain operations, such as string concatenation and substring operations. Because strings are immutable, the original string can be left unchanged while a new string is created with the desired modifications.
但也不是所有时候都必须要用.join(iterable), 随着join性能好,但是+它readability更高,如果是one-time use, 不妨用+. I choose readability over performance 99% of the case
Code
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
paths = []
stack = [(root, str(root.val))]
while stack:
# unpack stack
node, path = stack.pop()
# reach leaf node
if not node.left and not node.right:
# 只在reach leaf node时,写入
paths.append(path)
if node.left:
stack.append((node.left, '->'.join([path, str(node.left.val)])))
# stack.append((node.left, path + '->' + str(node.left.val)))
if node.right:
stack.append((node.right, '->'.join([path, str(node.right.val)])))
# string immutable, the above
# stack.append((node.right, path + '->' + str(node.right.val)))
return paths